Difference between revisions of "Fuzzy logic language"
Gianfranco (talk | contribs) |
Gianfranco (talk | contribs) |
||
| Line 107: | Line 107: | ||
Given the whole universe <math>U</math> we indicate with <math>x</math> its generic element such that<math>x \in U</math>; then we consider two subsets <math>A</math> and <math>B</math> internal to <math>U</math> such that <math>A \subset U</math> and <math>B \subset U</math> | Given the whole universe <math>U</math> we indicate with <math>x</math> its generic element such that<math>x \in U</math>; then we consider two subsets <math>A</math> and <math>B</math> internal to <math>U</math> such that <math>A \subset U</math> and <math>B \subset U</math> | ||
{| | {| | ||
| − | |[[File:Venn0111.svg|sinistra| | + | |[[File:Venn0111.svg|sinistra|80px]] |
|'''Union:''' represented by the symbol <math>\cup</math>, indicates the union of the two sets <math>A</math> and <math>B</math> <math>(A\cup B)</math>. It is defined by all the elements that belong to <math>A</math> and <math>B</math> or both: | |'''Union:''' represented by the symbol <math>\cup</math>, indicates the union of the two sets <math>A</math> and <math>B</math> <math>(A\cup B)</math>. It is defined by all the elements that belong to <math>A</math> and <math>B</math> or both: | ||
<math>(A\cup B)=\{\forall x\in U \mid x\in A \land x\in B\}</math> | <math>(A\cup B)=\{\forall x\in U \mid x\in A \land x\in B\}</math> | ||
|- | |- | ||
| − | |[[File:Venn0001.svg|sinistra| | + | |[[File:Venn0001.svg|sinistra|80px]] |
|'''Intersection:''' represented by the symbol <math>\cap</math>, indicates the elements belonging to both sets: | |'''Intersection:''' represented by the symbol <math>\cap</math>, indicates the elements belonging to both sets: | ||
<math>(A\cap B)=\{\forall x\in U \mid x\in A \lor x\in B\}</math> | <math>(A\cap B)=\{\forall x\in U \mid x\in A \lor x\in B\}</math> | ||
|- | |- | ||
| − | |[[File:Venn0010.svg|sinistra| | + | |[[File:Venn0010.svg|sinistra|80px]] |
|'''Difference:''' represented by the symbol <math>-</math>, for example <math>A-B</math> shows that all elements of <math>A</math> except those shared with <math>B</math> | |'''Difference:''' represented by the symbol <math>-</math>, for example <math>A-B</math> shows that all elements of <math>A</math> except those shared with <math>B</math> | ||
|- | |- | ||
| − | |[[File:Venn1000.svg|sinistra| | + | |[[File:Venn1000.svg|sinistra|80px]] |
|'''Complementary:''' represented by a bar above the name of the collection, it indicates by <math>\bar{A}</math> the complementary of <math>A</math>, that is, the set of elements that belong to the whole universe except those of <math>A</math>, in formulas: <math>\bar{A}=U-A</math><br /> | |'''Complementary:''' represented by a bar above the name of the collection, it indicates by <math>\bar{A}</math> the complementary of <math>A</math>, that is, the set of elements that belong to the whole universe except those of <math>A</math>, in formulas: <math>\bar{A}=U-A</math><br /> | ||
|}The theory of fuzzy language logic is an extension of the classical theory of sets in which, however, the principles of non-contradiction and the excluded third are not valid. Remember that in classical logic, given the set <math>A</math> and its complementary <math>\bar{A}</math>, the principle of non-contradiction states that if an element belongs to the whole <math>A</math> it cannot at the same time also belong to its complementary <math>\bar{A}</math>; according to the principle of the excluded third, however, the union of a whole <math>A</math> and its complementary <math>\bar{A}</math> constitutes the complete universe <math>U</math>. | |}The theory of fuzzy language logic is an extension of the classical theory of sets in which, however, the principles of non-contradiction and the excluded third are not valid. Remember that in classical logic, given the set <math>A</math> and its complementary <math>\bar{A}</math>, the principle of non-contradiction states that if an element belongs to the whole <math>A</math> it cannot at the same time also belong to its complementary <math>\bar{A}</math>; according to the principle of the excluded third, however, the union of a whole <math>A</math> and its complementary <math>\bar{A}</math> constitutes the complete universe <math>U</math>. | ||
Revision as of 19:26, 29 March 2021
In this chapter, we will discuss fuzzy logic. It is called fuzzy because it is characterized by a gradualness: an object can be attributed a quality that can have various degrees of truth.
In the first part of this chapter, the meaning of graded truth will be conceptually discussed, while in the second part, we will delve into the mathematical formalism by introducing the membership function : the element that allows us to mathematically synthesize the nuances of this logic of language. The conclusion has a positive aspect. It has been possible to show that with ‘fuzzy’ reasoning, unlike the previous logics of language, the diagnoses show less uncertainty. Despite this, however, the need is still felt to further refine the language method and enrich it with further ‘logics’.
Introduction
We have come this far because we, as colleagues, are very often faced with responsibilities and decisions that are very difficult to take and issues such as conscience, intelligence and humility come into play. n such a situation, however, we are faced with two equally difficult obstacles to manage that of one ( Knowledge Basis) as we discussed in the chapter ‘Logic of probabilistic language’, limited in the time we sign and one limited in the specific context (). These two parameters of epistemology characterize the scientific age in which we live. Also, both that the are dependent variables of our phylogeny, and, in particular of our conceptual plasticity and attitude to change.[1]
(I'll give you a practical example)
How much research has been produced on the topic 'Fuzzy logic'?
Pubmed responds with 2862 articles in the last 10 years[2], so that we can say that ours is current and is sufficiently updated. However, if we wanted to focus attention on a specific topic like ‘Temporomandibular Disorders’, the database will respond with as many as 2,235 articles. [3] Hence, if we wanted to check another topic like ‘Orofacial Pain’, Pubmed gives us 1,986 articles.[4] This means that the for these three topics in the last 10 years it has been sufficiently updated.
If, now, we wanted to verify the interconnection between the topics we will notice that in the contexts it will be the following:
- 'Temporomandibular disorders AND Orofacial Pain' 9 articles in the last 10 years[5]
- 'Temporomandibular disorders AND Orofacial Pain AND Fuzzy logic' 0 articles in the last 10 years [6]
The example shown means that the it is relatively up-to-date individually for the three topics while it decreases dramatically when the topics between contexts are merged and specifically to 9 articles for Point 1) and even to 0 articles for Point 2). So, the is a time dependent variable while the is a cognitive variable dependent on our aptitude for the progress of science, as already mentioned—among other things—in the chapter ‘Introduction’.
(Wait and see)
We ended the previous chapter by asserting that the logic of a classical language and subsequently probabilistic logic have helped us a lot in the progress of medical science and diagnostics but implicitly carry within themselves the limits of their own logic of language, which limits the vision of the biological universe. We also verified that with the logic of a classical language—so to speak, Aristotelian—the logical syntax that is derived from it in the diagnostics of our Mary Poppins limits, in fact, the clinical conclusion.
( see chapter Classical Language's Logic),
argues that: "every normal patient which is positive on the radiographic examination of the TMJ has TMDs, from this it follows that Mary Poppins being positive (and also being a "normal" patient) on the TMJ x-ray then Mary Poppins is also affected by TMDs
The limitation of the logical path that has been followed has led us to undertake an alternative path, in which the bivalence or binary nature of classical language logic is avoided and a probabilistic model is followed. The dentist colleague, in fact, changed the vocabulary and preferred a conclusion like:
and which is, that our Mary Poppins is 95% affected by TMDs since she has a degeneration of the temporomandibular joint supported by the positivity of the data in a population sample . However, we also found that in the process of constructing probabilistic logic (Analysandum ) which allowed us to formulate the aforementioned differential diagnostic conclusions and choose the most plausible one, there is a crucial element to the whole Analysand represented by the term which indicates, specifically, a 'Knowledge Base' of the context on which the logic of probabilistic language is built.
We therefore concluded that perhaps the dentist colleague should have become aware of his own 'Subjective Uncertainty' (affected by TMDs or nOP?) and 'Objective Uncertainty' (probably more affected by TMDs or nOP?).
Why have we come to these critical conclusions?
For a widely shared form of the representation of reality, supported by the testimony of authoritative figures who confirm its criticality. This has given rise to a vision of reality which, at first glance, would seem unsuitable for medical language; in fact, expressions such as ‘about 2’ or ‘moderately’ can arouse legitimate perplexity and seem an anachronistic return to pre-scientific concepts. On the contrary, however, the use of fuzzy numbers or assertions allows scientific data to be treated in contexts in which one cannot speak of ‘probability’ but only of ‘possibility’.[7]
Graduated truth
In the ambitious attempt to mathematically translate human rationality, it was thought in the mid-twentieth century to expand the concept of classical logic by formulating fuzzy logic. Fuzzy logic concerns the properties that we could call ‘graduate’, i.e., which can be attributed to an object with different degrees. Examples are the properties ‘being sick’, ‘having pain’, ‘being tall’, ‘being young’, and so on.
Mathematically, fuzzy logic allows you to attribute to each proposition a degree of truth between and . The most classic example to explain this concept is that of age: we can say that a new-born has a ‘degree of youth’ equal to , an eighteen-year-old equal to , a sixty-year-old equal to , and so on ...
In the context of classical logic, on the other hand, the statements:
- a ten-year-old is young
- a thirty-year-old is young
are both true. However, in the case of classical logic (which allows only the two true or false data), this would mean that the infant and the thirty-year-old are equally young. Which is obviously wrong.
The importance and the charm of fuzzy logic arise from the fact that it is able to translate the uncertainty inherent in some data of human language into mathematical formalism, coding ‘elastic’ concepts (such as almost high, fairly good, etc.), in order to make them understandable and manageable by computers. .
Set theory
As mentioned in the previous chapter, the basic concept of fuzzy logic is that of multivalence, i.e., in terms of set theory, of the possibility that an object can belong to a set even partially and, therefore, also to several sets with different degrees. Let us recall from the beginning the basic elements of the theory of ordinary sets. As will be seen, in them appear the formal expressions of the principles of Aristotelian logic, recalled in the previous chapter.
Quantifiers
- Membership: represented by the symbol (belongs), - for example the number 13 belongs to the set of odd numbers
- Non-membership: represented by the symbol (It does not belong).
- Inclusion: Represented by the symbol (is content), - for example the whole it is contained within the larger set , (in this case it is said that is a subset of ).
- Universal quantifier, which is indicated by the symbol (for each).
- Demonstration, which is indicated by the symbol (such that)
Set operators
Given the whole universe we indicate with its generic element such that; then we consider two subsets and internal to such that and
The theory of fuzzy language logic is an extension of the classical theory of sets in which, however, the principles of non-contradiction and the excluded third are not valid. Remember that in classical logic, given the set and its complementary , the principle of non-contradiction states that if an element belongs to the whole it cannot at the same time also belong to its complementary ; according to the principle of the excluded third, however, the union of a whole and its complementary constitutes the complete universe .
In other words, if any element does not belong to the whole, it must necessarily belong to its complementary.
Fuzzy set and membership function
We choose - as a formalism - to represent a fuzzy set with the 'tilde':. A fuzzy set is a set where the elements have a 'degree' of belonging (consistent with fuzzy logic): some can be included in the set at 100%, others in lower percentages.
To mathematically represent this degree of belonging is the function called 'Membership Function'. The function is a continuous function defined in the interval where it is:
- if is totally contained in (these points are called 'nucleus', they indicate plausible predicate values).
- if is not contained in
- if is partially contained in (these points are called 'support', they indicate the possible predicate values).
The graphical representation of the function it can be varied; from those with linear lines (triangular, trapezoidal) to those in the shape of bells or 'S' (sigmoidal) as depicted in Figure 1, which contains the whole graphic concept of the function of belonging.[8][9]
The support set of a fuzzy set is defined as the zone in which the degree of membership results ; on the other hand, the core is defined as the area in which the degree of belonging assumes value
The 'Support set' represents the values of the predicate deemed possible, while the 'core' represents those deemed more plausible.
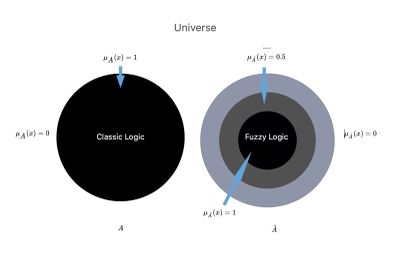
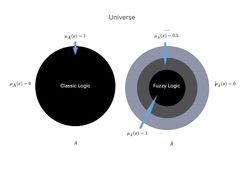
If represented a set in the ordinary sense of the term or classical language logic previously described, its membership function could assume only the values or , depending on whether the element whether or not it belongs to the whole, as considered. Figure 2 shows a graphic representation of the crisp (rigidly defined) or fuzzy concept of membership, which clearly recalls Smuts's considerations.[10] Let us go back to the specific case of our Mary Poppins, in which we see a discrepancy between the assertions of the dentist and the neurologist and we look for a comparison between classical logic and fuzzy logic:
Figure 2: Let us imagine the Science Universe in which there are two parallel worlds or contexts, and .
In the scientific context, the so-called ‘crisp’, and we have converted into the logic of Classic Language, in which the physician has an absolute scientific background information with a clear dividing line, we signed
In another scientific context called ‘fuzzy logic’, and in which there is a union between the subset in that we can go so far as to say: union between .
We will remarkably notice the following deductions:
- Classical Logic in the Dental Context in which only a logical process that gives as results it will be possible, or being the range of data reduced to basic knowledge in the set . This means that outside the dental world there is a void and that term of set theory, it is written precisely and which is synonymous with a high range of:
- Fuzzy logic in a dental context in which they are represented beyond the basic knowledge of the dental context also those partially acquired from the neurophysiological world will have the prerogative to return a result and a result because of basic knowledge which at this point is represented by the union of dental and neurological contexts. The result of this scientific-clinical implementation of dentistry would allow a:«Reduction of differential diagnostic error»
Final considerations
topics that could distract the reader’s attention—was, in fact, essential for demonstrating the message. Normally, in fact, when any more or less brilliant mind allows itself to throw a stone into the pond of Science, a shockwave is generated, typical of the period of Kuhn’s extraordinary science, against which most of the members of the international scientific community row. With good faith, we can say that this phenomenon—as regards the topics we are addressing here—is well represented in the premise at the beginning of the chapter.
In these chapters, in fact, a fundamental topic for science has been approached: the re-evaluation, the specific weight that has always been given to , awareness of scientific / clinical contexts , having undertaken a more elastic path of Fuzzy Logic than the Classical one, realizing the extreme importance of and ultimately the union of contexts to increase its diagnostic capacity.
In the next chapter we will be ready to undertake an equally fascinating path that will leads us to the context of a System Language logic and will allow us to deepen our knowledge no longer only in clinical semeiotics but in the understanding of system functions (in our case it is the Masticatory System.
- ↑ Takeuchi S, Okuda S, «Knowledge base toward understanding actionable alterations and realizing precision oncology», in Int J Clin Oncol, 2019.
PMID:30542800 - PMCID:PMC6373253
DOI:10.1007/s10147-018-1378-0
This is an Open Access resource - ↑ Fuzzy logic on Pubmed
- ↑ Temporomandibular Disorders in Pubmed
- ↑ Orofacial Pain in Pubmed
- ↑ Temporomandibular disorders AND Orofacial Pain in Pubmed
- ↑ "Temporomandibular disorders AND Orofacial Pain AND Fuzzy logic" in Pubmed
- ↑ Dubois D, Prade H, «Fundamentals of Fuzzy Sets», Kluwer Academic Publishers, 2000, Boston.
- ↑ Zhang W, Yang J, Fang Y, Chen H, Mao Y, Kumar M, «Analytical fuzzy approach to biological data analysis», in Saudi J Biol Sci, 2017.
PMID:28386181 - PMCID:PMC5372457
DOI:10.1016/j.sjbs.2017.01.027 - ↑ Lazar P, Jayapathy R, Torrents-Barrena J, Mol B, Mohanalin, Puig D, «Fuzzy-entropy threshold based on a complex wavelet denoising technique to diagnose Alzheimer disease», in Healthc Technol Lett, The Institution of Engineering and Technology, 2016.
PMID:30800318 - PMCID:PMC6371778
DOI:10.1049/htl.2016.0022 - ↑ •SMUTS J.C. 1926, Holism and Evolution, London: Macmillan.
particularly focusing on the field of the neurophysiology of the masticatory system

















































![{\displaystyle [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3bf59a5da5d8181083b228c8933efbda133483)