Difference between revisions of "The logic of classical language/es"
Gianfranco (talk | contribs) (Created page with "Para simplificar la exposición y la lectura, en este capítulo trataremos el ''símbolo de pertenencia'', el ''símbolo de consecuencia'' y el ''tal que'' como si fueran cuan...") |
Gianfranco (talk | contribs) (Created page with "Estrictamente hablando, dentro de la lógica clásica no deben ser tratados como tales, pero aunque lo hagamos, esto no cambia absolutamente el sentido del discurso y no se cr...") |
||
| Line 455: | Line 455: | ||
''‘Afortunadamente, las proposiciones matemáticas, si están bien expresadas, no presentan tales ambigüedades’.'' | ''‘Afortunadamente, las proposiciones matemáticas, si están bien expresadas, no presentan tales ambigüedades’.'' | ||
| − | Las proposiciones más simples pueden combinarse entre sí para formar nuevas proposiciones más complejas. Esto ocurre con la ayuda de operadores llamados ''operadores lógicos'' y conectivos cuantificadores que pueden reducirse a lo siguiente<ref>Para simplificar la exposición y la lectura, en este capítulo trataremos el ''símbolo de pertenencia'', el ''símbolo de consecuencia'' y el ''tal que'' como si fueran cuantificadores y conectivas de proposiciones en la lógica clásica.<br> | + | Las proposiciones más simples pueden combinarse entre sí para formar nuevas proposiciones más complejas. Esto ocurre con la ayuda de operadores llamados ''operadores lógicos'' y conectivos cuantificadores que pueden reducirse a lo siguiente<ref>Para simplificar la exposición y la lectura, en este capítulo trataremos el ''símbolo de pertenencia'', el ''símbolo de consecuencia'' y el ''tal que'' como si fueran cuantificadores y conectivas de proposiciones en la lógica clásica.<br>Estrictamente hablando, dentro de la lógica clásica no deben ser tratados como tales, pero aunque lo hagamos, esto no cambia absolutamente el sentido del discurso y no se crean incoherencias de ningún tipo.</ref>: |
#''Conjunction'', which is indicated by the symbol <math>\land</math> (and): | #''Conjunction'', which is indicated by the symbol <math>\land</math> (and): | ||
Revision as of 03:14, 27 October 2021
En conclusión, es evidente que una lógica clásica del lenguaje, que tiene un enfoque extremadamente dicotómico (o algo es blanco, o es negro), no puede describir los muchos matices que tienen las situaciones clínicas reales.
Como pronto veremos, este trabajo mostrará que la lógica clásica carece de la precisión necesaria, lo que nos obliga a mejorarla con otros tipos de lenguajes lógicos.
Introducción
Nos habíamos separado en el capítulo anterior sobre la 'Lógica del lenguaje médico' en un intento de desplazar la atención del síntoma o signo clínico al lenguaje de máquina encriptado para lo cual, los argumentos de Donald E Stanley, Daniel G Campos y Pat Croskerry son bienvenidos pero conectados al tiempo como portador de información (anticipación del síntoma) y al mensaje como lenguaje de máquina y no como lenguaje no verbal).[1][2]
Obviamente, esto no excluye la validez de la historia clínica construida sobre un lenguaje verbal pseudo-formal a estas alturas bien arraigado en la realidad clínica y que ya ha demostrado su autoridad diagnóstica. El intento de trasladar la atención a un lenguaje de máquina y al Sistema no proporciona más que una oportunidad para la validación de la Ciencia Médica de Diagnóstico.
Definitivamente, somos conscientes de que nuestro Sapiens Linux sigue perplejo ante lo que se ha anticipado y continúa preguntándose
(un poco de paciencia, por favor)
No podemos dar una respuesta convencional porque la ciencia no avanza con afirmaciones que no estén justificadas por preguntas y reflexiones científicamente validadas; y esta es la razón por la que trataremos de dar voz a algunas reflexiones, perplejidades y dudas expresadas sobre algunos temas básicos puestos en discusión en algunos artículos científicos.
Uno de estos temas fundamentales es la "Biología Craneofacial"..
Empecemos con un conocido estudio de Townsend y Brook[3]: en esta obra los autores cuestionan el status quo de la investigación tanto fundamental como aplicada en "Biología Craneofacial" para extraer consideraciones e implicaciones clínicas. Uno de los temas que trataron fue el "Enfoque Interdisciplinario", en el que Geoffrey Sperber y su hijo Steven vieron la fuerza del progreso exponencial de la 'Biología Craneofacial' en innovaciones tecnológicas como la secuenciación de genes, la tomografía computarizada, las imágenes de resonancia magnética, el láser de barrido, el análisis de imágenes, la ultrasonografía y la espectroscopia[4].
Otro tema de gran interés para la aplicación de la "Biología Craneofacial" es la conciencia de que los sistemas biológicos son "Sistemas Complejos[5] y que la "epigenética" desempeña un papel clave en la biología molecular craneofacial. Investigadores de Adelaida y Sydney ofrecen una revisión crítica en el campo de la epigenética dirigida, de hecho, a las disciplinas dentales y craneofaciales.[6] La fenómica, en particular, discutida por estos autores (véase Fenómica) es un campo de investigación general que implica la medición de los cambios en los dientes y las estructuras orofaciales asociadas resultantes de las interacciones entre los factores genéticos, epigenéticos y ambientales durante el desarrollo.[7] En este mismo contexto, cabe destacar el trabajo de Irma Thesleff, de Helsinki (Finlandia). En su trabajo explica que hay una serie de centros de señalización transitoria en el epitelio dental que desempeñan importantes funciones en el programa de desarrollo de los dientes.[8] Además hay otros trabajos, de Peterkova R, Hovor akova M, Peterka M, Lesot H, que proporcionan una fascinante revisión de los procesos que ocurren durante el desarrollo dental;[9][10][11] en aras de la exhaustividad, no olvidemos los trabajos de Han J, Menicanin D, Gronthos S, y Bartold PM., que revisan una amplia documentación sobre las células madre, la ingeniería de tejidos y la regeneración periodontal.[12]
En esta revisión no podían faltar los argumentos sobre las influencias genéticas, epigenéticas y ambientales durante la morfogénesis que conducen a variaciones en el número, tamaño y forma del diente[13][14] y la influencia de la presión lingual en el crecimiento y la función craneofacial.[15][16]
El extraordinario trabajo de Townsend y Brook también merece una mención[3], y el contenido intrínseco de lo relatado en él coincide igualmente con otro autor encomiable: HC Slavkin.[17] Slavkin afirma que:
- "El futuro está lleno de importantes oportunidades para mejorar los resultados clínicos de las malformaciones craneofaciales congénitas y adquiridas. Los clínicos desempeñan un papel fundamental, ya que el pensamiento crítico y la audiencia clínica mejoran sustancialmente la precisión del diagnóstico y, por tanto, los resultados clínicos en materia de salud."
(Le daré un ejemplo práctico)
En el capítulo "Introducción" planteamos ciertas preguntas sobre el tema de la maloclusión pero en este contexto simulamos la lógica del lenguaje médico del dentista ante el caso clínico presentado en el "capítulo de introducción" con sus conclusiones diagnósticas y terapéuticas.
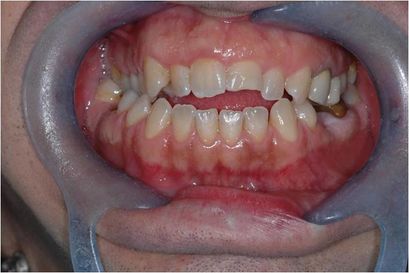
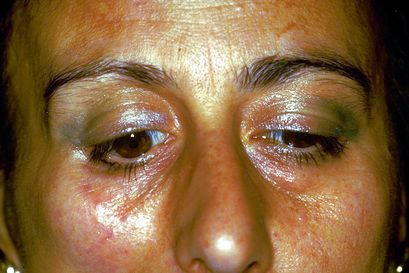
El paciente tiene una mordida cruzada unilateral posterior y una mordida abierta anterior.[18] La mordida cruzada es otro elemento perturbador de la oclusión normal[19] por lo que se trata obligatoriamente junto con la mordida abierta.[20][21] Este tipo de razonamiento significa que el modelo (sistema masticatorio) está "normalizado a la oclusión"; y leído al revés, significa que la discrepancia oclusal es la causa de la maloclusión, por lo tanto, una enfermedad del Sistema Masticatorio, y por lo tanto una intervención para restaurar la función masticatoria fisiológica es justificable. (Figura 1a).
Este ejemplo es el Lenguaje Lógico Clásico, como vamos a explicar en detalle, pero ahora surge una duda:
- En la época en que los axiomas de la ortodoncia y la ortognática construían protocolos confirmados por la Comunidad Científica Internacional, ¿conocían la información de la que hablamos en la introducción de este capítulo?
Ciertamente no porque el tiempo es el portador de la información pero a pesar de este límite cognitivo se procede con una Lógica del Lenguaje Clásico muy cuestionable para la seguridad del ciudadano.
(Claro, pero la secuencia lógica ya se ha anticipado)
Si el mismo caso se interpretara con una mentalidad que siguiera una "lógica del lenguaje del sistema" (se tratará en el capítulo correspondiente), las conclusiones serían sorprendentes.
Si observamos las respuestas electrofisiológicas realizadas al paciente con maloclusión en las figuras 1b, 1c y 1d (con la explicación hecha directamente en el pie de foto para simplificar la discusión), nos daremos cuenta de que estos datos pueden hacernos pensar en cualquier cosa menos en una 'Maloclusión' y, por tanto, los axiomas de tipo ortodóntico y ortognático 'causa/efecto' dejan un vacío conceptual.
(Lo haremos siguiendo el caso clínico de nuestra Mary Poppins)
particularly focusing on the field of the neurophysiology of the masticatory system
Formalismo matemático
En este capítulo, vamos a reconsiderar el caso clínico de la desafortunada Mary Poppins que sufre de dolor orofacial desde hace más de 10 años y a la que su dentista diagnosticó un "Trastorno Temporomandibular" (TTM) o más bien dolor orofacial por TTM. Para entender mejor por qué la formulación diagnóstica exacta sigue siendo compleja con una Lógica del Lenguaje Clásico, debemos entender el concepto en el que se basa la filosofía del lenguaje clásico con una breve introducción al tema.
Proposiciones
La lógica clásica se basa en las proposiciones. A menudo se dice que una proposición es una frase que pregunta si la proposición es verdadera o falsa. De hecho, una proposición en matemáticas suele ser verdadera o falsa, pero esto es obviamente demasiado vago para ser una definición. Puede tomarse, en el mejor de los casos, como una advertencia: si una frase, expresada en el lenguaje común, no tiene sentido preguntar si es verdadera o falsa, no será una proposición sino otra cosa.
Se puede discutir si las frases del lenguaje común son o no proposiciones, ya que en muchos casos no suele ser evidente si una determinada afirmación es verdadera o falsa.
‘Afortunadamente, las proposiciones matemáticas, si están bien expresadas, no presentan tales ambigüedades’.
Las proposiciones más simples pueden combinarse entre sí para formar nuevas proposiciones más complejas. Esto ocurre con la ayuda de operadores llamados operadores lógicos y conectivos cuantificadores que pueden reducirse a lo siguiente[22]:
- Conjunction, which is indicated by the symbol (and):
- Disjunction, which is indicated by the symbol (or):
- Negation, which is indicated by the symbol (not):
- Implication, which is indicated by the symbol (if ... then):
- Consequence, which is indicated by the symbol (is a partition of..):
- Universal quantifier, which is indicated by the symbol (for all):
- Demonstration, which is indicated by the symbol (such that): and
- Membership, which is indicated by the symbol (is an element of) or by the symbol (is not an element of):
Demonstration by absurdity
Furthermore, in classical logic there is a principle called the excluded third which declares that a sentence that cannot be false must be taken as true since there is no third possibility.
Suppose we need to prove that the proposition is true. The procedure consists in showing that the assumption that is false leads to a logical contradiction. Thus the proposition cannot be false, and therefore, according to the law of the excluded third, it must be true. This method of demonstration is called demonstration by absurdity[23]
Predicates
What we have briefly described so far is the logic of propositions. A proposition asserts something about specific mathematical objects such as: '2 is greater than 1, so 1 is less than 2' or 'a square has no 5 sides then a square is not a pentagon'. Many times, however, the mathematical statements concern not the single object, but generic objects of a set such as: ' are taller than 2 meters' where denotes a generic group (for example all volleyball players). In this case we speak of predicates.
Intuitively, a predicate is a sentence concerning a group of elements (which in our medical case will be the patients) and which states something about them.
(let's see what Classical Language Logic tells us)
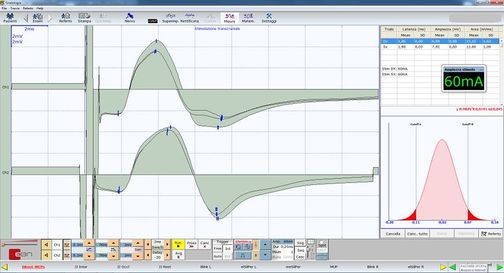
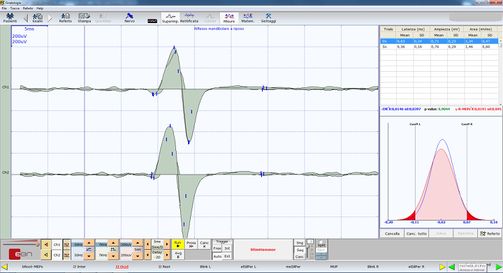
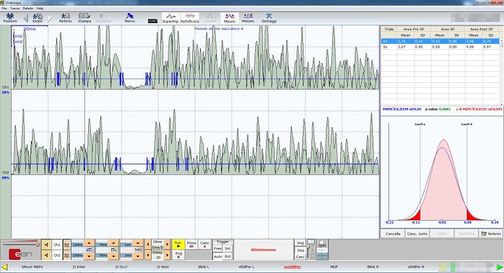
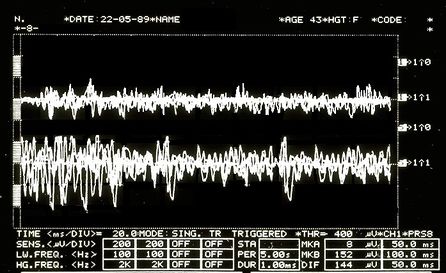
In addition to the confirmations derived from the logic of medical language discussed in the previous chapter, the dentist colleague acquires other instrumental data that allow him to confirm his diagnosis. The latter tests concern the analysis of the axiographic traces by using a customized functional paraocclusal clutch which allow the visualization and quantification of the condylar traces in masticatory functions. As can be seen from Figure 4 the flattening of the condylar traces on the right side both in the mediotrusive masticatory kinetics (green colour) and the opening and protrusion cycles (gray colour) confirm the anatomical and functional flattening of the right TMJ in the dynamics chewing. In addition to the axiography, the colleague performs a surface electromyography on the masseters (Fig. 6) asking the patient to exert the maximum of his muscles force. This type of electromyographic analysis is called "EMG Interferential Pattern" due to the high frequency content of the spikes that undergo phase interference. In fact, Figure 6 shows an asymmetry in the recruitment of the motor units of the right masseter (upper trace) compared to those of the left masseter (lower trace).[24][25][26][27]
2nd Clinical Approach
(Hover over the images)
Dental propositions
While seeking to use the mathematical formalism to translate the conclusions reached by the dentist with classical logic language, we consider the following predicates:
- x Normal patients (normal stands for patients commonly present in the specialist setting)
- Bone remodelling with osteophyte from stratigraphic examination and condylar CT; and
- Temporomandibular Disorders (TMDs) resulting in Orofacial Pain (OP)
- Specific patient: Mary Poppins
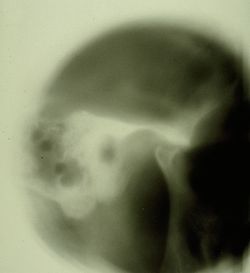
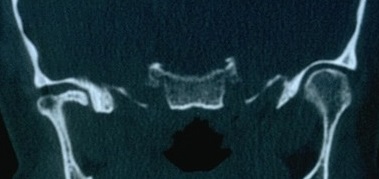
Any normal patient who is positive on the radiographic examination of the TMJ [Figure 2 and 3] is affected by TMDs ; from this it follows that being Mary Poppins positive (and also being a "Normal" patient) on the TMJ x-ray then Mary Poppins is also affected by TMDs
The language of predicates is expressed in the following way:
.
At this point, it must also be considered that predicate logic is not used only to prove that a particular set of premises imply a particular evidence . It is also used to prove that a particular assertion is not true, or that a particular piece of knowledge is logically compatible/incompatible with a particular evidence.
In order to prove that this proposition is true we must use the above mentioneddemonstration by absurdity. If its denial creates a contradiction, surely the dentist's proposition will be true:
.
"" states that it is not true that those who test positive on TMJ CT have TMDs, so Mary Poppins (TMJ CT positive normal patient) does not have TMDs.
The dentist believes that Mary Poppins' claim (that she does not have TMD under these premises) is a contradiction so the main claim is true.
Neurophysiological proposition
Let us imagine that the neurologist disagrees with the conclusion and asserts that Mary Poppins is not affected by TMDs or that at least it is not the main cause of Orofacial Pain, but that, rather, she is affected by a neuromotor Orofacial Pain (nOP), therefore that she does not belong to the group of 'normal patients' but is to be considered a 'non-specific patient' (uncommon in the specialist context).
Obviously, this dialectic would last indefinitely because both would defend their scientific-clinical context; but let us see what happens in the logic of predicates.
The neurologist's statement would be like:
.
"" means that every patient who is TMJ CT positive has TMDs but even though Mary Poppins is TMJ CT positive, she does not have TMDs.
In order to prove that this proposition is true, we must use once again the above mentioned demonstration by absurdity. If its denial creates a contradiction, surely the neurologist's proposition will be true:
.
Following the logical rules of predicates, there is no reason to say that denial (4) is contradictory or meaningless, therefore the neurologist (unlike the dentist) would not seem to have the logical tools to confirm his conclusion.
Compatibility and incompatibility of the statements
The complication lies in the fact that the dentist will present a series of statements as clinical reports such as the stratigraphy and CT of the TMJ, that indicate an anatomical flattening of the joint, axiography of the condylar traces with a reduction in kinematic convexity and a tracing EMG interference pattern in which an asymmetrical pattern on the masseters is highlighted. These assertions can easily be considered a contributing cause of the damage to the Temporomandibular Joint and, therefore, responsible for the 'Orofacial pain'.
Documents, reports and clinical evidence can be used to make the neurologist's assertion incompatible and the dentist's diagnostic conclusion compatible. To do this we must present some logical rules that describe the compatibility or incompatibility of the logic of classical language:
- A set of sentences , and a number of other phrases or statements are logically compatible if, and only if, the union between them is coherent.
- A set of sentences , and a number of other phrases or statements are logically incompatible if, and only if, the union between them is incoherent.
Let us try to follow this reasoning with practical examples:
The dentist colleague exposes the following sentence:
: Following the personalized techniques suggested by Xin Liang et al.[28] who focuses on the quantitative microstructural analysis of the fraction of the bone value, the trabecular number, the trabecular thickness and the trabecular separation on each slice of the CT scan of a TMJ, it appears that Mary Poppins is affected by Temporomandibular Disorders (TMDs) and the consequence causes Orofacial Pain.
At this point, however, the thesis must be confirmed with further clinical and laboratory tests, and in fact the colleague produces a series of assertions that should pass the compatibility filter as described above, namely:
Bone remodelling: The flattening of the axiographic traces highlighted in figure 5 indicates the joint remodelling of the right TMJ of Mary Poppins, such a report can be correlated to a series of researches and articles that confirm how malocclusion can be associated with morphological changes in the temporomandibular joints, particularly when combined with the age as the presence of a chronic malocclusion can worsen the picture of bone remodelling.[29] These scientific references determine the compatibility of the assertion.
Sensitivity and specificity of the axiographic measurement: A study was conducted to verify the sensitivity and specificity of the data collected from a group of patients affected by temporomandibular joint disorders with an ARCUSdigma axiographic system[30]; it confirmed a sensitivity of the 84.21% and a 92.86% sensitivity for the right and left TMJs respectively, and a specificity of 93.75% and 95.65%.[31] These scientific references determine compatibility of the assertion in the dental context precisely because of the consistency of related studies.[32]
Alteration of condylar paths: Urbano Santana-Mora and coll.[33] evaluated 24 adult patients suffering from severe chronic unilateral pain diagnosed as Temporomandibular Disorders (TMDs). The following functional and dynamic factors were evaluated:
- masticatory function;
- remodelling of the TMJ or condylar pathway (CP); and
- lateral movement of the jaw or lateral guide (LG).
The CPs were assessed using conventional axiography and LG was assessed by using kinesiograph tracing[34]; Seventeen (71%) of the 24 (100%) patients consistently showed a side of habitual chewing side. The mean and standard deviation of the CP angles was 47.90 9.24) degrees. The average of LG angles was 42.9511.78 degrees.
Data collection emerged from the conception of a new TMD paradigm in which the affected side could be the usual chewing side, the side where the mandibular lateral kinematic angle was flatter. This parameter may also be compatible with the dental claim.
EMG Intereference pattern: M.O. Mazzetto and coll.[35] showed that the electromyographic activity of the anterior temporal muscles and the masseter was positively correlated with the "Craniomandibular index", indiced (CMI) with a and suggesting that the use of CMI to quantify the severity of TMDs and EMG to assess the masticatory muscle function, may be an important diagnostic and therapeutic elements. These scientific references determine compatibility of the assertion.
?
Obviously, the dentist colleague could endlessly keep on casting his statements, indefinitely.
Well, all of these statements seem coherent with the sentence initially described, whereby the dentist colleague feels justified in saying that the set of sentences , and a number of other assertions or clinical data are logically compatible as the union between them is coherent.
(It would seem so!
But, be careful, only in his own dental context!)
This statement is so true that the could be infinitely extended, widened enough to obtain an that corresponds to it in an infinite significance, as long as it remains limited in its context; yet, without meaning anything from a clinical point of view in other contexts, like in the neurologist one, for instance.
Final considerations
From a perspective of observation of this kind, the Logic of Predicates can only fortify the dentist’s reasoning and, at the same time, strengthen the principle of the excluded third: the principle is strengthened through the compatibility of the additional assertions which grant the dentist a complete coherence in the diagnosis and in confirming the sentence : Poor Mary Poppins either has TMD, or she has not.
Basically, given the compatibility of the assertions , coherently saying that Orofacial Pain is caused by a Temporomandibular Disorders could become incompatible if another series of assertions were shown to be coherent: this would make a different sentence compatible : could poor Mary Poppins suffer from Orofacial Pain from a neuromotor disorder (nOP) and not by a Temporomandibular Disorders?
In the current medical language logic, such assertions only remain assertions, because the convictions and opinions do not allow a consequent and quick change of the mindset.
Moreover, taking into account the risk that this change entails, in fact, we might consider a recent article on the epidemiology of temporomandibular disorders[36] in which the authors confirm that despite the methodological and population differences, pain in the temporomandibular region appears to be relatively common, occurring in about the 10% of the population; we may then objectively be led to hypothesize that our Mary Poppins can be included in the 10% of the patients mentioned in the epidemiological study, and contextually be classified as a patient suffering from Orofacial Pain from Temporomandibular Disorders (TMDs).
In conclusion, it is evident that a classical logic of language, which has an extremely dichotomous approach (either it is white or it is black), cannot depict the many shades that occur in real clinical situations.
We need to find a more convenient and suitable language logic...
- ↑ Stanley DE, Campos DG, «The logic of medical diagnosis», in Perspect Biol Med, 2013.
PMID:23974509
DOI:10.1353/pbm.2013.0019 - ↑ Croskerry P, «Adaptive expertise in medical decision making», in Med Teach, 2018.
PMID:30033794
DOI:10.1080/0142159X.2018.1484898 - ↑ 3.0 3.1 Townsend GC, Brook AH, «The face, the future, and dental practice: how research in craniofacial biology will influence patient care», in Aust Dent J, Australian Dental Association, 2014.
PMID:24646132
DOI:10.1111/adj.12157 - ↑ Sperber GH, Sperber SM, «The genesis of craniofacial biology as a health science discipline», in Aust Dent J, Australian Dental Association, 2014.
PMID:24495071
DOI:10.1111/adj.12131 - ↑ Brook AH, Brook O'Donnell M, Hone A, Hart E, Hughes TE, Smith RN, Townsend GC, «General and craniofacial development are complex adaptive processes influenced by diversity», in Aust Dent J, Australian Dental Association, 2014.
PMID:24617813
DOI:10.1111/adj.12158 - ↑ Williams SD, Hughes TE, Adler CJ, Brook AH, Townsend GC, «Epigenetics: a new frontier in dentistry», in Aust Dent J, Australian Dental Association, 2014.
PMID:24611746
DOI:10.1111/adj.12155 - ↑ Yong R, Ranjitkar S, Townsend GC, Brook AH, Smith RN, Evans AR, Hughes TE, Lekkas D, «Dental phenomics: advancing genotype to phenotype correlations in craniofacial research», in Aust Dent J, Australian Dental Association, 2014.
PMID:24611797
DOI:10.1111/adj.12156 - ↑ Thesleff I, «Current understanding of the process of tooth formation: transfer from the laboratory to the clinic», in Aust Dent J, 2013.
DOI:10.1111/adj.12102 - ↑ Peterkova R, Hovorakova M, Peterka M, Lesot H, «Three‐dimensional analysis of the early development of the dentition», in Aust Dent J, Wiley Publishing Asia Pty Ltd on behalf of Australian Dental Association, 2014.
DOI:10.1111/adj.12130 - ↑ Lesot H, Hovorakova M, Peterka M, Peterkova R, «Three‐dimensional analysis of molar development in the mouse from the cap to bell stage», in Aust Dent J, 2014.
DOI:10.1111/adj.12132 - ↑ Hughes TE, Townsend GC, Pinkerton SK, Bockmann MR, Seow WK, Brook AH, Richards LC, Mihailidis S, Ranjitkar S, Lekkas D, «The teeth and faces of twins: providing insights into dentofacial development and oral health for practising oral health professionals», in Aust Dent J, 2013.
DOI:10.1111/adj.12101 - ↑ Han J, Menicanin D, Gronthos S, Bartold PM, «Stem cells, tissue engineering and periodontal regeneration», in Aust Dent J, 2013.
DOI:10.1111/adj.12100 - ↑ {{Cite book | autore = Brook AH | autore2 = Jernvall J | autore3 = Smith RN | autore4 = Hughes TE | autore5 = Townsend GC | titolo = The Dentition: The Outcomes of Morphogenesis Leading to Variations of Tooth Number, Size and Shape | url = https://onlinelibrary.wiley.com/doi/epdf/10.1111/adj.12160 | volume = | opera = Aust Dent J | anno = 2014 | editore = | città = | ISBN = | PMID = | PMCID = | DOI = 10.1111/adj.12160 | oaf = | LCCN = | OCLC =
- ↑ Seow WK, «Developmental defects of enamel and dentine: challenges for basic science research and clinical management», in Aust Dent J, 2014.
PMID:24164394
DOI:10.1111/adj.12104 - ↑ Kieser JA, Farland MG, Jack H, Farella M, Wang Y, Rohrle O, «The role of oral soft tissues in swallowing function: what can tongue pressure tell us?», in Aust Dent J, 2013.
DOI:10.1111/adj.12103 - ↑ Slavkin HC, «Research on Craniofacial Genetics and Developmental Biology: Implications for the Future of Academic Dentistry», in J Dent Educ, 1983.
PMID:6573384 - ↑ Slavkin HC, «The Future of Research in Craniofacial Biology and What This Will Mean for Oral Health Professional Education and Clinical Practice», in Aust Dent J, 2014.
PMID:24433547
DOI:10.1111/adj.12105 - ↑
Littlewood SJ, Kandasamy S, Huang G, «Retention and relapse in clinical practice», in Aust Dent J, 2017.
DOI:10.1111/adj.12475 - ↑ Miamoto CB, Silva Marques L, Abreu LG, Paiva SM, «Impact of two early treatment protocols for anterior dental crossbite on children’s quality of life», in Dental Press J Orthod, 2018.
- ↑ Alachioti XS, Dimopoulou E, Vlasakidou A, Athanasiou AE, «Amelogenesis imperfecta and anterior open bite: Etiological, classification, clinical and management interrelationships», in J Orthod Sci, 2014.
DOI:10.4103/2278-0203.127547 - ↑ Mizrahi E, «A review of anterior open bite», in Br J Orthod, 1978.
PMID:284793
DOI:10.1179/bjo.5.1.21 - ↑ Para simplificar la exposición y la lectura, en este capítulo trataremos el símbolo de pertenencia, el símbolo de consecuencia y el tal que como si fueran cuantificadores y conectivas de proposiciones en la lógica clásica.
Estrictamente hablando, dentro de la lógica clásica no deben ser tratados como tales, pero aunque lo hagamos, esto no cambia absolutamente el sentido del discurso y no se crean incoherencias de ningún tipo. - ↑ Pereira LM, Pinto AM, «Reductio ad Absurdum Argumentation in Normal Logic Programs», Arg NMR, 2007, Tempe, Arizona - Caparica, Portugal – in Argumentation and Non-Monotonic Reasoning - An LPNMR Workshop.
- ↑ Castroflorio T, Talpone F, Deregibus A, Piancino MG, Bracco P, «Effects of a Functional Appliance on Masticatory Muscles of Young Adults Suffering From Muscle-Related Temporomandibular Disorder», in J Oral Rehabil, 2004.
PMID:15189308
DOI:10.1111/j.1365-2842.2004.01274.x - ↑ Maeda N, Kodama N, Manda Y, Kawakami S, Oki K, Minagi S, «Characteristics of Grouped Discharge Waveforms Observed in Long-term Masseter Muscle Electromyographic Recording: A Preliminary Study», in Acta Med Okayama, Okayama University Medical School, 2019, Okayama, Japan.
PMID:31439959
DOI:10.18926/AMO/56938 - ↑ Rudy TE, «Psychophysiological Assessment in Chronic Orofacial Pain», in Anesth Prog, American Dental Society of Anesthesiology, 1990.
ISSN: 0003-3006/90
PMID:2085203 - PMCID:PMC2190318 - ↑ Woźniak K, Piątkowska D, Lipski M, Mehr K, «Surface electromyography in orthodontics - a literature review», in Med Sci Monit, 2013.
e-ISSN: 1643-3750
PMID:23722255 - PMCID:PMC3673808
DOI:10.12659/MSM.883927 - ↑ Liang X, Liu S, Qu X, Wang Z, Zheng J, Xie X, Ma G, Zhang Z, Ma X, «Evaluation of Trabecular Structure Changes in Osteoarthritis of the Temporomandibular Joint With Cone Beam Computed Tomography Imaging», in Oral Surg Oral Med Oral Pathol Oral Radiol, 2017.
PMID:28732700
DOI:10.1016/j.oooo.2017.05.514 - ↑ Solberg WK, Bibb CA, Nordström BB, Hansson TL, «Malocclusion Associated With Temporomandibular Joint Changes in Young Adults at Autopsy», in Am J Orthod, 1986.
PMID:3457531
DOI:10.1016/0002-9416(86)90055-2 - ↑ KaVo Dental GmbH, Biberach / Ris
- ↑ Kobs G, Didziulyte A, Kirlys R, Stacevicius M, «Reliability of ARCUSdigma (KaVo) in Diagnosing Temporomandibular Joint Pathology», in Stomatologija, 2007.
PMID:17637527 - ↑ Piancino MG, Roberi L, Frongia G, Reverdito M, Slavicek R, Bracco P, «Computerized axiography in TMD patients before and after therapy with 'function generating bites'», in J Oral Rehabil, 2008.
PMID:18197841
DOI:10.1111/j.1365-2842.2007.01815.x - ↑ López-Cedrún J, Santana-Mora U, Pombo M, Pérez Del Palomar A, Alonso De la Peña V, Mora MJ, Santana U, «Jaw Biodynamic Data for 24 Patients With Chronic Unilateral Temporomandibular Disorder», in Sci Data, 2017.
PMID:29112190 - PMCID:PMC5674825
DOI:10.1038/sdata.2017.168
This is an Open Access resource - ↑ Myotronics Inc., Kent, WA, US
- ↑ Oliveira Mazzetto M, Almeida Rodrigues C, Valencise Magri L, Oliveira Melchior M, Paiva G, «Severity of TMD Related to Age, Sex and Electromyographic Analysis», in Braz Dent J, 2014.
DOI:10.1590/0103-6440201302310 - ↑ LeResche L, «Epidemiology of temporomandibular disorders: implications for the investigation of etiologic factors», in Crit Rev Oral Biol Med, 1997.
PMID:9260045
DOI:10.1177/10454411970080030401
particularly focusing on the field of the neurophysiology of the masticatory system